نموذج انحدار ميتا للتأثيرات العشوائية

الوقت المقدّر للقراءة: 2 دقيقة

جدول المحتويات

نموذج انحدار ميتا للتأثيرات العشوائية

نموذج انحدار ميتا للتأثيرات العشوائية #

يستخدم المحلل إجراء الانحدار التلوي لتناسب نموذج الانحدار التلوي للتأثيرات العشوائية باستخدام البيانات المنظفة من ملف العينة glucose.sav والبنية النحوية التالية:

META REGRESSION LnRiskRatio with length
/DATA VAR=VARLnRiskRatio
/CRITERIA CILEVEL=95 CLASSMISSING=EXCLUDE MAXITER=200 MAXSTEP=100 CONVERGENCE=0.000001
/INFERENCE MODEL=RANDOM INTERCEPT=INCLUDE DISTRIBUTION=NORMAL ESTIMATE=ML ADJUSTSE=NONE
/PRINT COEFF_TEST PARAMETER.

لمعرفة المزيد، انتقل إلى treatSuccess ، و treatFailure ، و controlSuccess ، و controlFailure . يُشغّل المحلل الصيغة التالية لحساب نسبة المخاطرة اللوغاريتمية والتباين المقابل.

compute LnRiskRatio=LN(treatsuccess)-LN(treatSuccess+treatFailure)-LN(controlSuccess)+LN(controlSuccess+controlFailure).
compute VarLnRiskRatio=1/treatSuccess+1/controlSuccess-1/(treatSuccess+treatFailure)-1/(controlSuccess+controlFailure).
EXECUTE.

يتناول القسم التالي بالتفصيل كيفية حساب نسبة المخاطرة اللوغاريتمية والتباين المقابل من خلال ميزة حساب المتغير.

حساب نسبة المخاطرة والتباين اللوغاريتمي #

افتح ملف العينة glucose_length.sav.
لحساب نسبة المخاطرة اللوغاريتمية، اختر من القوائم: تحويل > حساب المتغير…

الشكل 1. مربع حوار حساب المتغير:

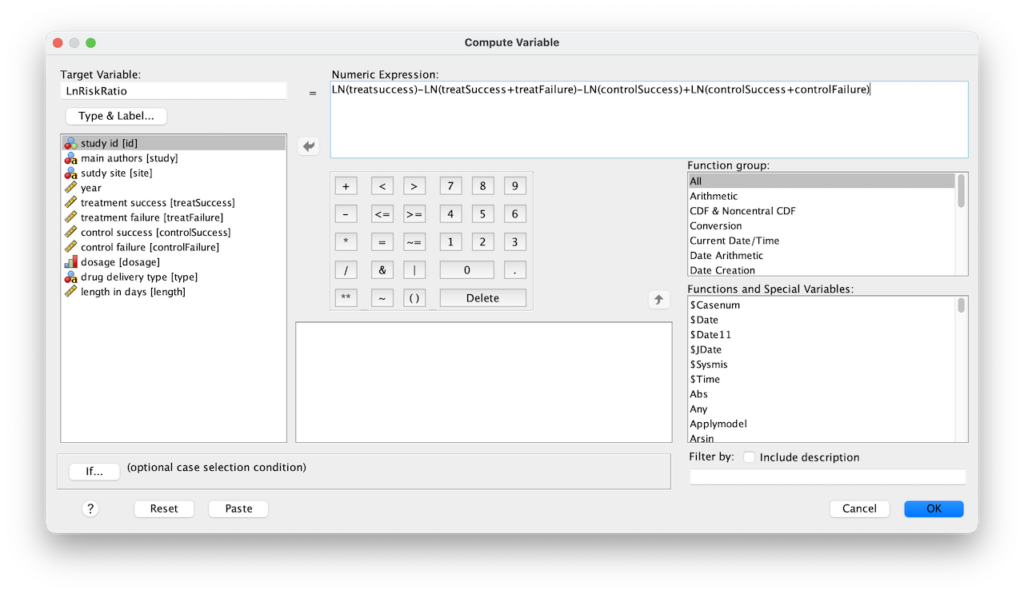
أدخل LnRiskRatio في حقل المتغير المستهدف، ثم قم بلصق المعادلة التالية في حقل التعبير الرقمي:

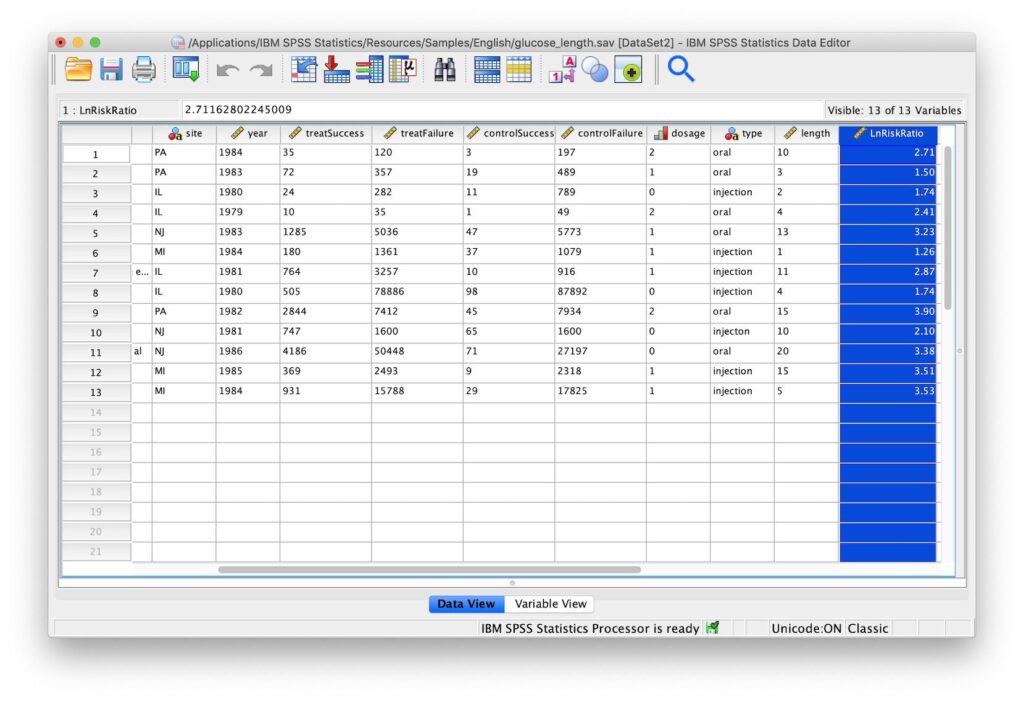
LN(treatsuccess)-LN(treatSuccess+treatFailure)-LN(controlSuccess)+LN(controlSuccess+controlFailure)

انقر فوق موافق. سيتم عرض المتغير الجديد LnRiskRatio في محرر البيانات.

الشكل 2. مربع حوار محرر البيانات مع تسليط الضوء على LnRiskRatio:

لحساب تباين نسبة المخاطرة اللوغاريتمية، اختر من القوائم: تحويل > حساب المتغير…

الشكل 3. مربع حوار حساب المتغير:

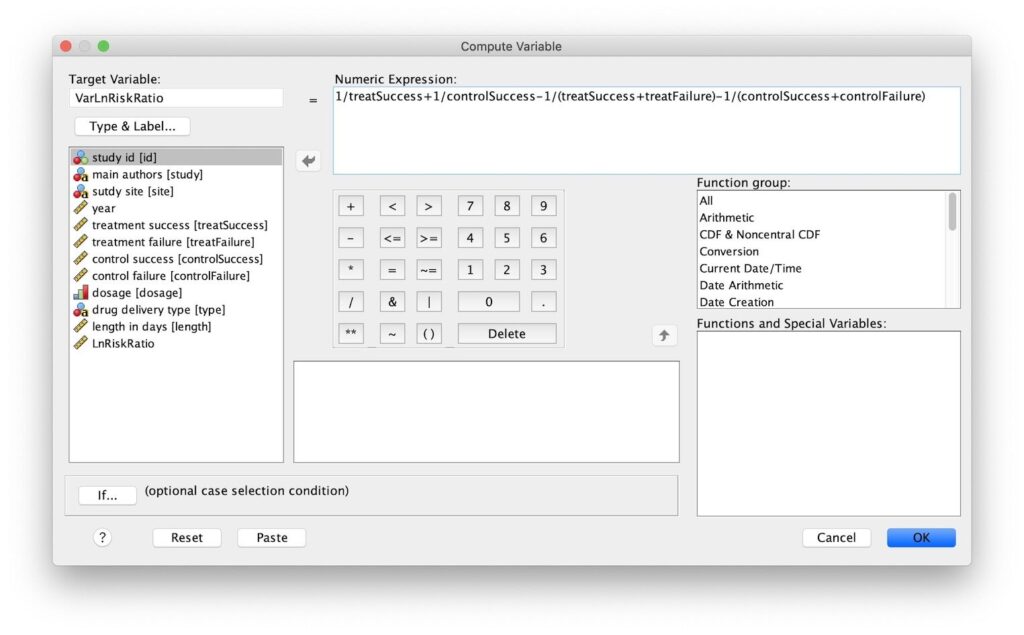
انقر فوق “إعادة تعيين” لمسح التعبير الرقمي المحدد.
أدخل VarLnRiskRatio في حقل المتغير المستهدف، ثم قم بلصق المعادلة التالية في حقل التعبير الرقمي:

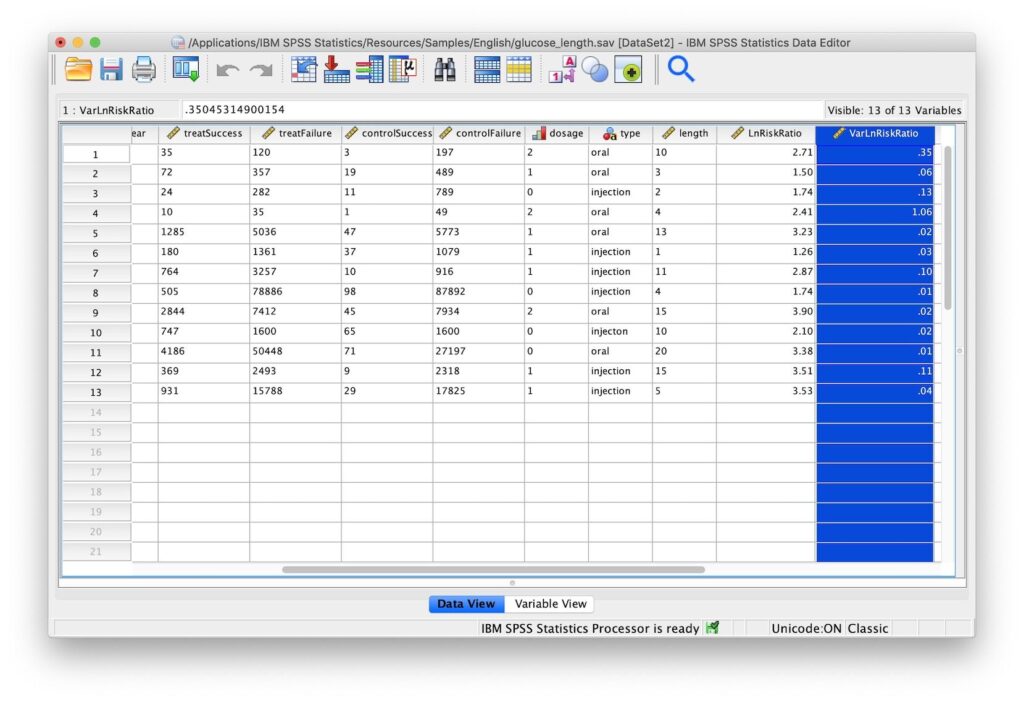
1/treatSuccess+1/controlSuccess-1/(treatSuccess+treatFailure)-1/(controlSuccess+controlFailure)

انقر فوق موافق. سيتم عرض المتغير الجديد VarLnRiskRatio في محرر البيانات.

الشكل 4. مربع حوار محرر البيانات مع تمييز VarLnRiskRatio:

يتناول القسم التالي بالتفصيل كيفية استخلاص الاستدلال الإحصائي حول التأثير من خلال إجراء التحليل التلوي: الانحدار.

تشغيل التحليل #

لتشغيل تحليل تلوي: تحليل الانحدار، اختر من القوائم: تحليل > تحليل تلوي > انحدار ميتا.

الشكل 5. التحليل التلوي: الحوار الرئيسي للانحدار

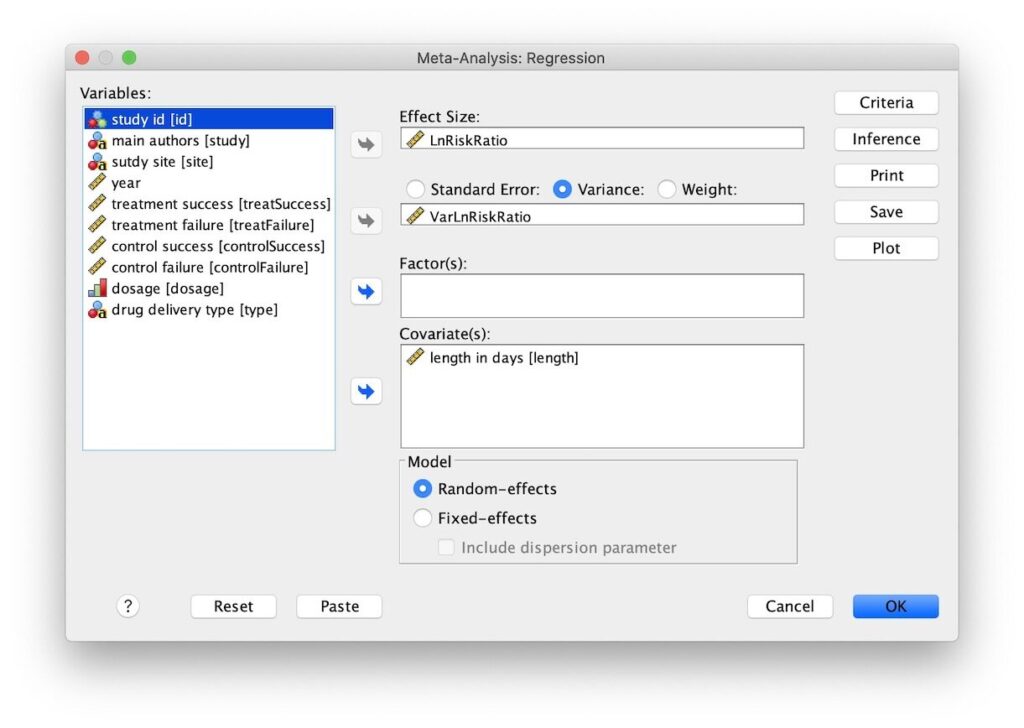
حدد LnRiskRatio كمتغير لحجم التأثير ، وحدد إعداد التباين و VarLnRiskRatio كمتغير يحدد التباين الذي يتم تحويله إلى الوزن، والطول بالأيام [length] كمتغير (ات) مشترك.
انقر فوق المعايير.

الشكل 6. مربع حوار المعايير:

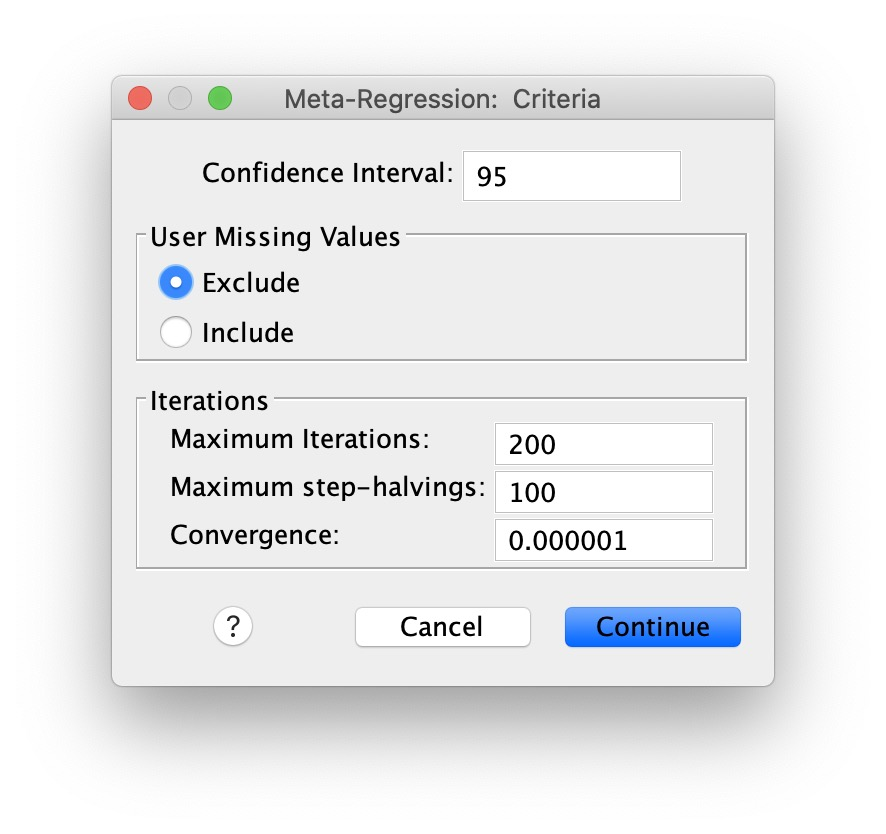
أدخل 200 في حقل الحد الأقصى للتكرارات .
أدخل 100 في حقل الحد الأقصى لنصف الخطوات .
انقر فوق متابعة .
انقر فوق الاستدلال .

الشكل 7. حوار الاستدلال:

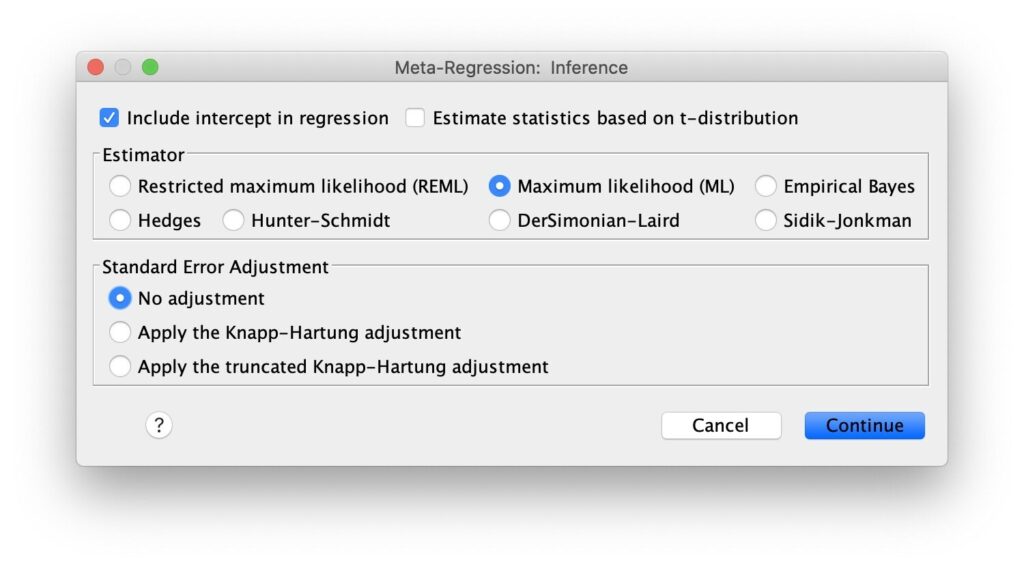
حدد إعدادات تضمين الاعتراض في الانحدار، والاحتمالية القصوى (ML)، وعدم التعديل .يقوم إعداد الاحتمالية القصوى (ML) ببناء نموذج الانحدار التلوي للتأثيرات العشوائية باستخدام طريقة الاحتمالية القصوى لتقدير التباين بين الدراسات.
انقر فوق متابعة.
انقر فوق طباعة.

الشكل 8. مربع حوار الطباعة:

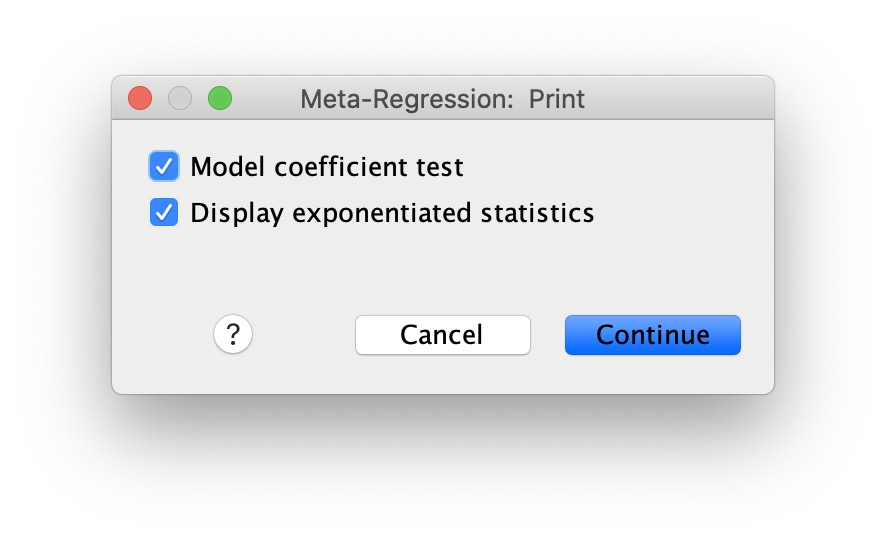
حدد إعدادات اختبار معامل النموذج وعرض الإحصائيات الأسيّة .
انقر فوق متابعة .
انقر فوق موافق .

جدول اختبار معامل النموذج #

يعرض جدول اختبار معاملات النموذج اختبارًا يفيد بأن جميع المعاملات، باستثناء نقطة التقاطع، تساوي 0 بناءً على اختبار مربع كاي لوالد. تبلغ قيمة اختبار مربع كاي لوالد 17.631، ومستوى الدلالة أقل من 0.001، مما يعني رفض الفرضية الصفرية القائلة بأن جميع المعاملات، باستثناء نقطة التقاطع، تساوي 0 عند مستوى الدلالة 0.05. بمعنى آخر، يجب قبول الفرضية البديلة القائلة بأن جميع المعاملات تختلف إحصائيًا عن 0.

جدول تقديرات المعلمات #

يُظهر جدول تقديرات المعاملات أن معامل طول المتغير بالأيام يساوي 0.117، مما يعني أن كل يوم طوله بالأيام يُقابل زيادة قدرها 0.117 وحدة في نسبة المخاطرة اللوغاريتمية. قيمة دلالة اختبار طول المتغير بالأيام أقل من 0.001، مما يشير إلى أن معامل طول المتغير بالأيام يختلف اختلافًا كبيرًا عن الصفر عند مستوى الدلالة 0.05.

ملاحظة: نظرًا لوجود وسيط واحد فقط (الطول بالأيام)، فإن اختبار

z يعادل اختبار Wald Chi-square في جدول اختبار معامل النموذج (قيمة Wald Chi-square تساوي قيمة z التربيعية ).

جدول اختبار التجانس المتبقي #

يوضح جدول اختبار التجانس المتبقي اختبار الفرضية القائلة بأن التباين بين الدراسات (مربع تاو) يساوي 0. تبلغ إحصائية اختبار مربع كاي 124.551 وقيمة الدلالة 0.000، مما يشير إلى وجود تباين بين المتبقيات.

جدول التباين المتبقي #

يُظهر جدول التباين المتبقي أن التباين بين الدراسات يُقدر بـ 0.275. تبلغ نسبة التباين (مربع I) 88.4%، ما يعني أن 88.4% من التباين في المتبقي يُعزى إلى التباين بين الدراسات، بينما يُعزى 11.6% إلى التباين داخل الدراسة. تبلغ قيمة R-squared 61.6%، ما يعني أن حوالي 61.6% من التباين بين الدراسات يُفسر بواسطة الوسيط (الطول بالأيام).