اختبار مساواة التباين الجماعي

اختبار مساواة التباين الجماعي #

تتمثل الخطوة الأولى المهمة في تحليل التباين الأحادي في إثبات صحة الافتراضات. أحد افتراضات ANOVA هو أن تباينات المجموعات متكافئة. يوضح المثال التالي كيفية إجراء هذا الاختبار.

يرغب مدير المبيعات في تحديد العدد الأمثل لأيام التدريب على المنتج اللازمة للموظفين الجدد. لديه درجات أداء لثلاث مجموعات: الموظفون الذين حصلوا على تدريب لمدة يوم أو يومين أو ثلاثة أيام. البيانات موجودة في الملف salesperformance.sav. راجع موضوع “ملفات الأمثلة” للحصول على مزيد من المعلومات.

مخطط المتوسطات والأخطاء القياسية #

قبل إجراء تحليل التباين الأحادي، نقوم برسم بياني للمتوسطات والأخطاء القياسية أو المعيارية standard errors.

1. لإنشاء مخطط الخطأ، اختر من القوائم: الرسوم البيانية> منشئ المخطط …

Graphs > Chart Builder…

2. حدد علامة التبويب المعرض Gallery، وحدد شريط Bar من قائمة أنواع المخططات.

3. قم بسحب وإسقاط رمز Simple Error Bar في منطقة اللوحة.

4. قم بسحب وإسقاط النتيجة في امتحان التدريب Score on training exam على المحور ص y axis.

5. انقر بزر الماوس الأيمن فوق مجموعة تدريب المبيعات Sales training group وحدد “اسمي” Nominal لمستوى القياس measurement level.

6. قم بسحب وإسقاط مجموعة تدريب المبيعات Sales training group على المحور س x axis.

الشكل التالي يبين شريط خطأ بسيط في مُنشئ المخططات Chart Builder:

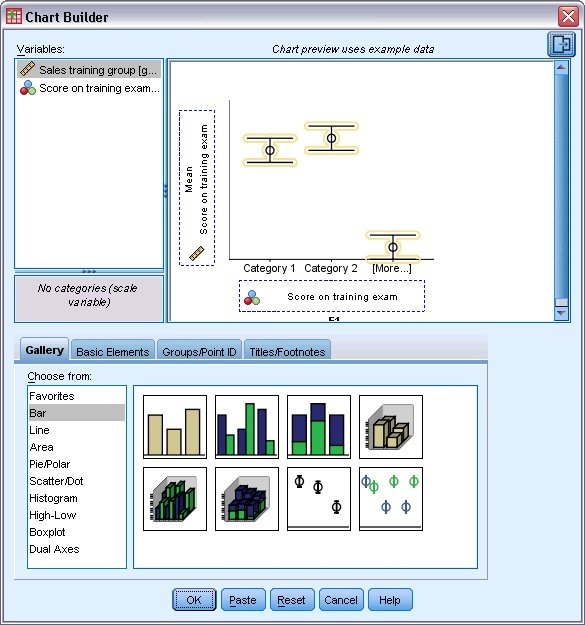
7. انقر فوق علامة التبويب خصائص العنصر Element Properties.

8. في المجموعة “تمثيل أشرطة الخطأ” Error Bars Represent، انقر فوق خطأ قياسي Standard Error.

يظهر مربع حوار منشئ المخططات، تحرير خصائص العنصر كما يلي:

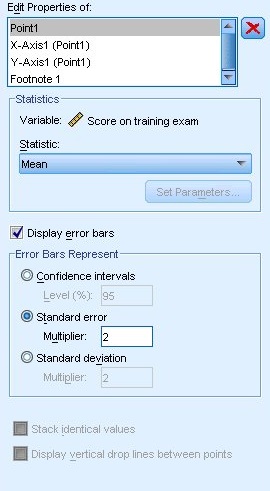
9. انقر فوق “موافق” OK في “منشئ المخطط” لإنشاء مخطط شريطي الخطأ.

يظهر مخطط شريطي للخطأ لدرجات الأداء حسب مجموعة التدريب كما يلي:

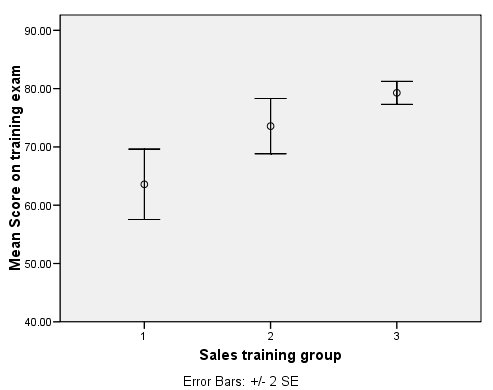
يزداد متوسط ​​الأداء بشكل واضح مع إضافة المزيد من أيام التدريب، لكن في نفس الوقت ينخفض الاختلاف في الأداء. يفترض One-Way ANOVA المساواة في التباين عبر المجموعات؛ قد لا يصح هذا الافتراض لهذه البيانات.

إجراء تحليل التباين أحادي الاتجاه #

لاختبار افتراض تكافؤ التباين :

1. اختر من القوائم: تحليل> مقارنة المتوسطات > تحليل التباين أحادي الاتجاه ANOVA …

Analyze > Compare Means > One-Way ANOVA…

يظهر مربع حوار تحليل التباين أحادي الاتجاه One-Way ANOVA كما يلي:

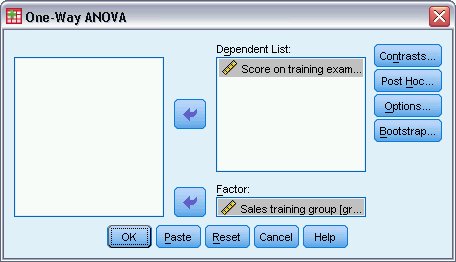
2. حدد الدرجة في امتحان التدريب أو Score on training exam كمتغير تابع dependent variable.

3. حدد مجموعة تدريب المبيعات أو Sales training group كمتغير عاملي factor variable.

4. انقر فوق خيارات Options.

يظهر مربع حوار الخيارات لإجراء تحليل One-Way ANOVA كما يلي:

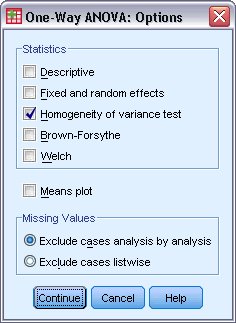
5. حدد اختبار تجانس التباين أو Homogeneity of variance test.

6. انقر فوق متابعة Continue.

7. انقر فوق “موافق” OK في مربع حوار تحليل التباين أحادي الاتجاه أو One-Way ANOVA.

جدول الإحصاء الوصفي #

الشكل التالي يبين جدول الإحصاء الوصفي لتحليل التباين أحادي الاتجاه One-way ANOVA descriptive statistics table:

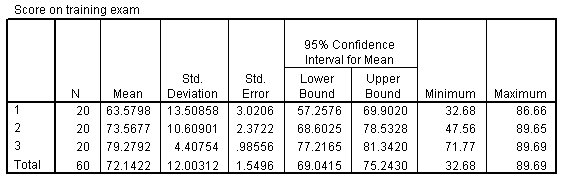
تؤكد إحصائيات الانحراف المعياري أو standard deviation والخطأ المعياري standard error أنه مع زيادة أيام التدريب، ينخفض التباين في الأداء.

جدول اختبار ليفين Levene #

الشكل التالي يبين إحصائيات تجانس جدول التباين أو Homogeneity of variance table:

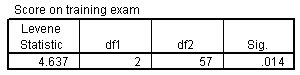
ترفض إحصائية ليفين Levene الفرضية الصفرية بأن تباينات المجموعة متساوية. يعتبر ANOVA قويًا في مواجهة هذا الانتهاك عندما تكون المجموعات متساوية أو قريبة من التساوي في الحجم؛ ومع ذلك، يمكنك اختيار تحويل البيانات أو إجراء اختبار غير معلمي nonparametric test لا يتطلب هذا الافتراض.